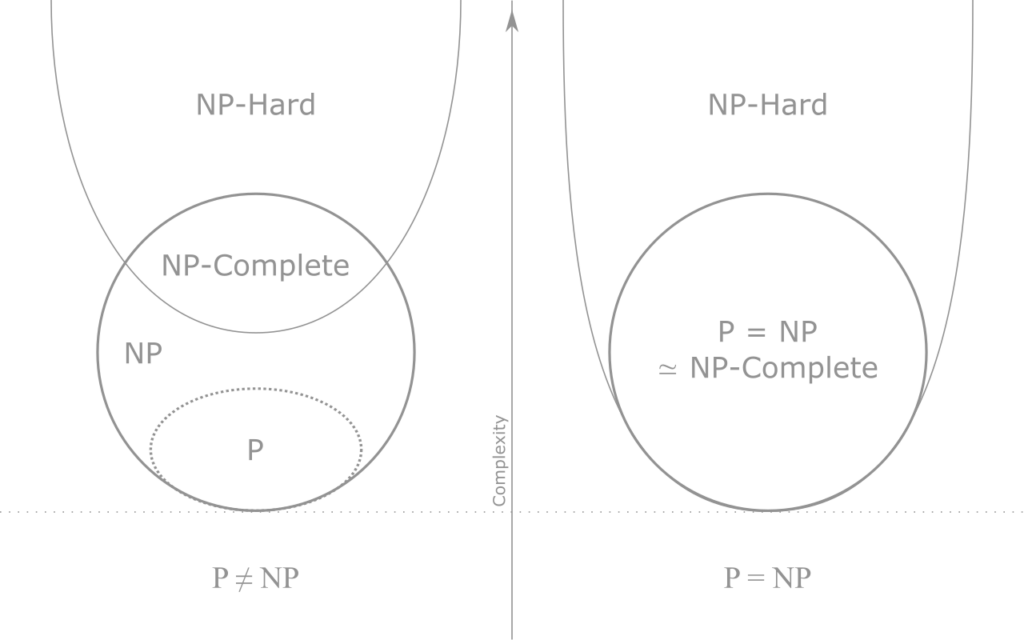
Предложенное доказательство того, что P≠NP вызвало больший интерес, чем ожидалось. Итак, как это происходит и что это говорит обо всем процессе науки в эпоху вики. У нас есть обновление.
Новость (Доказательство P≠NP) О том, что предложенное доказательство того, что P не равно NP, опубликованная в Интернете ранее на этой неделе, вызвала больший интерес, чем можно было представить, от такой сухой академической проблемы. Конечно, если вы понимаете, какое значение имеет доказательство того, что P≠NP, то это не так уж сухо, академично и проблемно.
Всего через несколько дней после того, как доказательство было обнародовано, первые комментарии были собраны в хорошо известном (в кругах компьютерных наук) блоге Godel’s Lost Letter and P=NP. В блоге все сказано, но, по сути, есть возражения против доказательства — но в любом новом сложном доказательстве всегда будет много технических возражений. Вопрос в том, можно ли свести эти технические объекты к чему-то менее вредному для доказательства.
Что, возможно, менее известно о реальном процессе математического доказательства, так это то, что он включает в себя не только логику, но и социальное согласие. Математики должны принять доказательство, чтобы оно приобрело статус доказательства. Принятие в основном означает, что специалисты в данной области видят, что даже если в доказательстве есть ошибки, их можно исправить, немного поработав. Иногда эти небольшие проблемы возвращаются, чтобы уничтожить доказательства в последующие годы, когда то, что на первый взгляд кажется очевидным, оказывается неразрешимым.
Блог документирует усилия по проработке статьи. Доказательство работает от противоречия. Он предполагает, что P=NP, а затем показывает, что это означает, что существует алгоритм с полиномиальным временем определенного типа. Далее в статье показано, что это приводит к противоречию из-за известных статистических свойств случайных k-SAT экземпляров для больших k. Задачи k-SAT заключаются в том, чтобы определить, может ли данная логическая формула быть истинной путем подходящего присвоения переменных. Многие возражения против статьи сосредоточены на том, было ли достигнуто противоречие или пропущен пункт «убирайся».
До сих пор ни одно из возражений не было сокрушительным ударом по доказательству, и автор Винай Деолаликар поддерживает свою работу. Была создана вики-страница, чтобы предлагать и обрабатывать проблемы с доказательством, и Деолаликар регулярно выпускает обновления для статьи.
В настоящее время кажется, что доказательство неверно и не может быть исправлено незначительными переделками, но оно, вероятно, открывает совершенно новый путь к решению таких проблем, как NP=P, и со временем может привести к доказательству.
Что не менее увлекательно для компьютерных ученых, да и вообще для всех ученых, так это то, как Интернет заметно изменил способ ведения науки. Открытое «протестное» рассмотрение, обсуждение и общее пережевывание этой статьи совершенно не похоже на то, что ученый признал бы экспертной оценкой всего несколько лет назад.
Это также является толчком для развития информатики — предмета, который в последние несколько лет теряет популярность среди студентов, программистов и даже ученых.