Есть некоторые новости прошлого года, которые заслуживают второго шанса. Вот одна из них — хотя она не так известна, как давно известная гипотеза P=NP, проблема Коллатца увлекала людей на протяжении последних восьми десятилетий и дала почти столько же ошибочных доказательств. Теперь математик Теренс Тао, похоже, близок к доказательству.
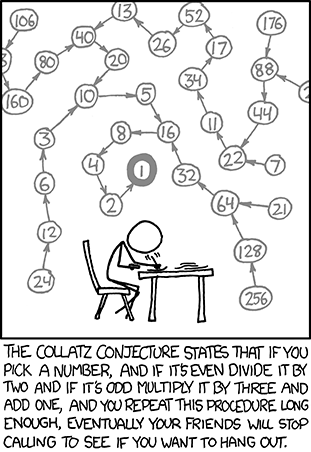
Если вы не знаете, что такое гипотеза Коллатца, то вы не пропустили ничего действительно важного — за исключением, возможно, отличного мультфильма xkcd, воспроизведенного ниже:
Карикатура точная, но давайте проясним догадку, предложенную в 1937 году немецким математиком Лотаром Коллатцем:
- Выберите число, целое положительное число.
- Если четное — разделите на 2
- Если нечетное — умножьте на 3 и прибавьте единицу
- Повторите два вышеуказанных шага с новым значением
Если вы попробуете это сделать, то обнаружите, что в конечном итоге вы достигнете результата 1. Например, 10, 5,16, 8, 4, 2, 1. Сначала вы думаете, что это, должно быть, случайность, и поэтому пробуете еще несколько тестов. Затем вы становитесь одержимым и пишете программу — и в итоге всегда получаете 1.
До сих пор это было проверено для значений вплоть до 5,76×10^18.
По предположению Коллатца, это действительно всегда так, но можете ли вы это доказать?
Если вы думаете, что это должно быть легко, то стоит знать, что Пол Эрдёс провозгласил:
Математика может быть не готова к таким проблемам
Теренс Тао из Калифорнийского университета близок к доказательству, как никогда раньше. Почему это не доказательство? Потому что это вероятностный аргумент:
Почти все орбиты карты Коллатца достигают почти ограниченных значений.
Почему это важно? Причина в том, что если вы можете показать, что минимум последовательности Коллатца для N всегда меньше N при всех N>1, то вы доказали гипотезу Коллатца. Причина проста. Если вы получите значение m, которое меньше N, то остальная часть последовательности для N будет такой же, как если бы вы начали с m, и таким образом мы получим, что минимум последовательности меньше m. Вы можете повторить это и вернуться назад, чтобы доказать, что минимум должен быть равен 1.
Тао не совсем доказал это, но он доказал (переписано, чтобы быть ближе к английскому):
Теорема 2: Пусть f — любая функция, определенная на целых числах, исключая нуль, и f(N) уходит в бесконечность с N, тогда минимум последовательности Коллатца для N меньше, чем f(N) для почти всех N.
Если принять f за тождество, то получается, что минимальное значение Коллатца для N меньше N.
Значит, проблема решена?
Не совсем. Ласковое слово в теореме — «почти для всех». Это сигнал о том, что теорема носит вероятностный характер. Это означает, что множество N, для которого это верно, является плотным (в смысле логарифмической плотности). В нетехническом смысле это означает, что мы доказали, что теорема верна для всех случаев, кроме незначительного числа.
Незначительное число случаев также включает в себя отсутствие случаев вообще, так что теорема может быть применима ко всем N, или может быть несколько примеров, где она не применима, и предположение Коллатца все-таки неверно.
Так что же из этого следует?
Как пишет Тао в ответе на комментарий к его статье в блоге:
…но это одна из тех ситуаций, когда между «почти всеми» результатами и «всеми» результатами существует огромный разрыв в сложности
Похоже, что гипотеза Коллатца продержится еще некоторое время. Вооружившись этим вероятностным аргументом, можно найти новые причины, почему она верна.