Если вы используете антибиотики против бактерий, устойчивость к антибиотикам неизбежна. Однако, если вы умело используете несколько антибиотиков, вы можете настроить популяцию бактерий, чтобы она оставалась неизменной. Этот алгоритмический подход к управлению эволюцией — один из способов сохранить полезность антибиотиков для будущих поколений, а также имеет более широкое применение.
Если вы используете один антибиотик против популяции бактерий, вы убьете большую часть или все организмы, которые к нему восприимчивы. Немногочисленные оставшиеся в живых бактерии образуют начало новой популяции, устойчивой к антибиотику. Это эволюция в действии. Когда популяция подвергается давлению, наиболее приспособленные организмы выживают и увеличиваются в пропорции к целому. Обратите внимание, что это произойдет, даже если антибиотики не будут злоупотреблять. Чрезмерное употребление ускоряет процесс, но ограничение в использовании антибиотиков в конечном итоге приводит к резистентности.
По данным Центров по контролю и профилактике заболеваний CDC, ежегодно более 2 миллионов человек в Соединенных Штатах заболевают инфекциями, устойчивыми к антибиотикам, и по меньшей мере 23000 человек умирают в результате этого.
Один из подходов к использованию антибиотиков во избежание отбора по устойчивости — это чередование используемых антибиотиков. Таким образом вы надеетесь избежать применения единого эволюционного давления, чтобы заставить население двигаться в направлении устойчивости к какому-либо конкретному или нескольким антибиотикам.
Если перевести эту слепую ротацию на более сложный уровень, что, если бы мы могли разработать оптимальные графики использования антибиотиков, которые поддерживали бы популяцию в ее первоначальном состоянии и даже возвращали бы устойчивую популяцию обратно в дикое состояние? Мириам Барлоу из Калифорнийского университета в Мерседе и математик Кристина Крона из Американского университета в Вашингтоне, округ Колумбия, сделали именно это — и алгоритм интересен и, возможно, его можно улучшить.
Сохранение простоты биологии означает, что мы можем сосредоточиться на алгоритме. Если вы хотите узнать подробности, см. Статью на веб-сайте Plos One.
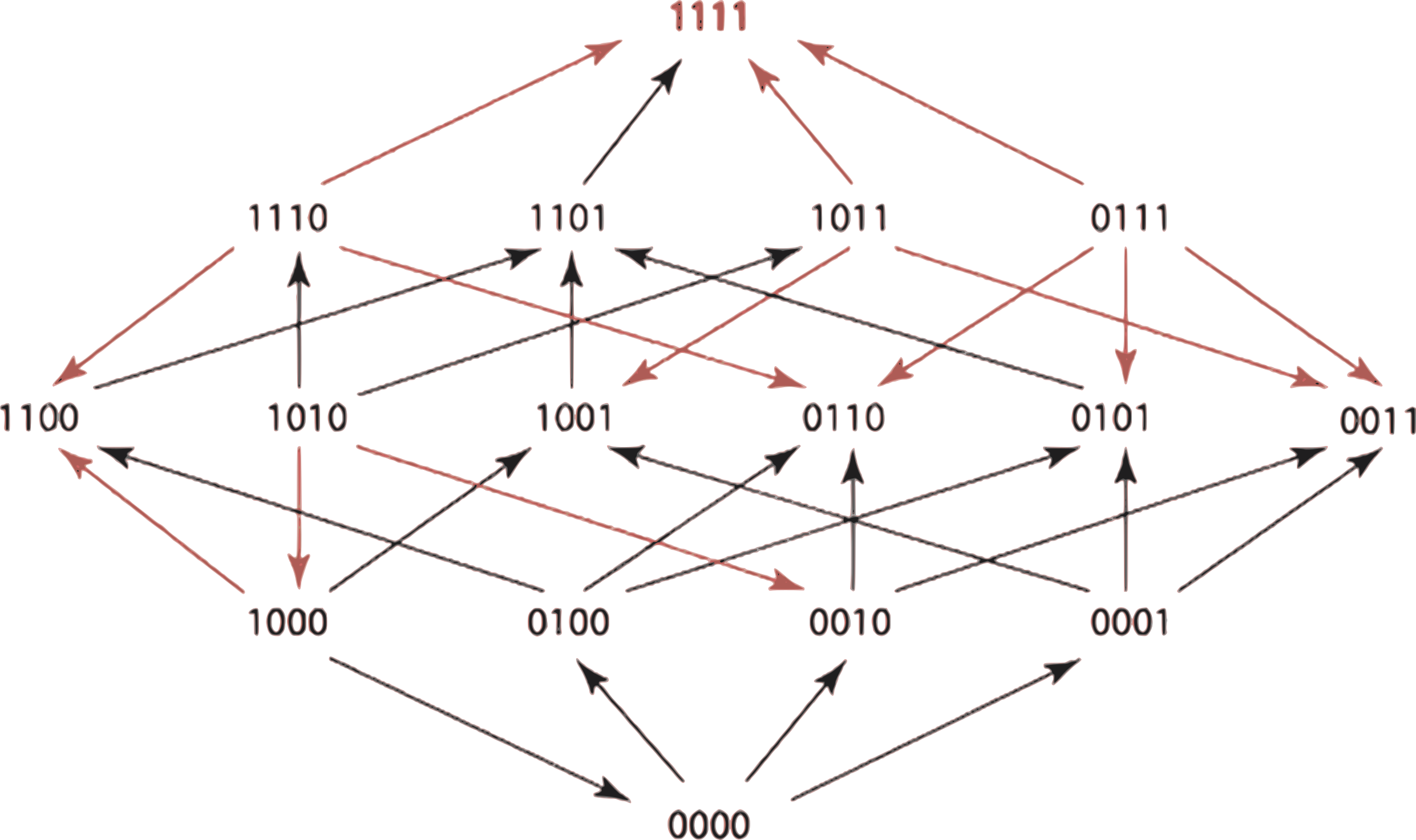
В исследовании рассматривались четыре возможных замены аминокислот, каждая из которых придает некоторую устойчивость к антибиотикам. Мы можем идентифицировать генотип как четырехбитное число, где 0000 является диким типом, а 1 означает замену. Если мы предположим, что вероятность замены низкая, то мы можем предположить, что в любой момент времени происходит только одно изменение. Это означает, что генотипы образуют простой граф Хэмминга. То есть у нас есть граф с 16 узлами и связями между узлами, которые отличаются на один бит, то есть они находятся на расстоянии одного расстояния Хэмминга. Вы можете измерить эволюционное давление любого данного антибиотика, измерив тенденцию любого генотипа к уменьшению в пользу генотипа, который отличается на одну аминокислоту. Например, для ампициллина мы имеем следующий граф Хэмминга:
Красные стрелки указывают на существенные различия в скорости роста. Вы можете думать о красных стрелках как об эволюционных изменениях, которые, вероятно, связаны с применением антибиотика.
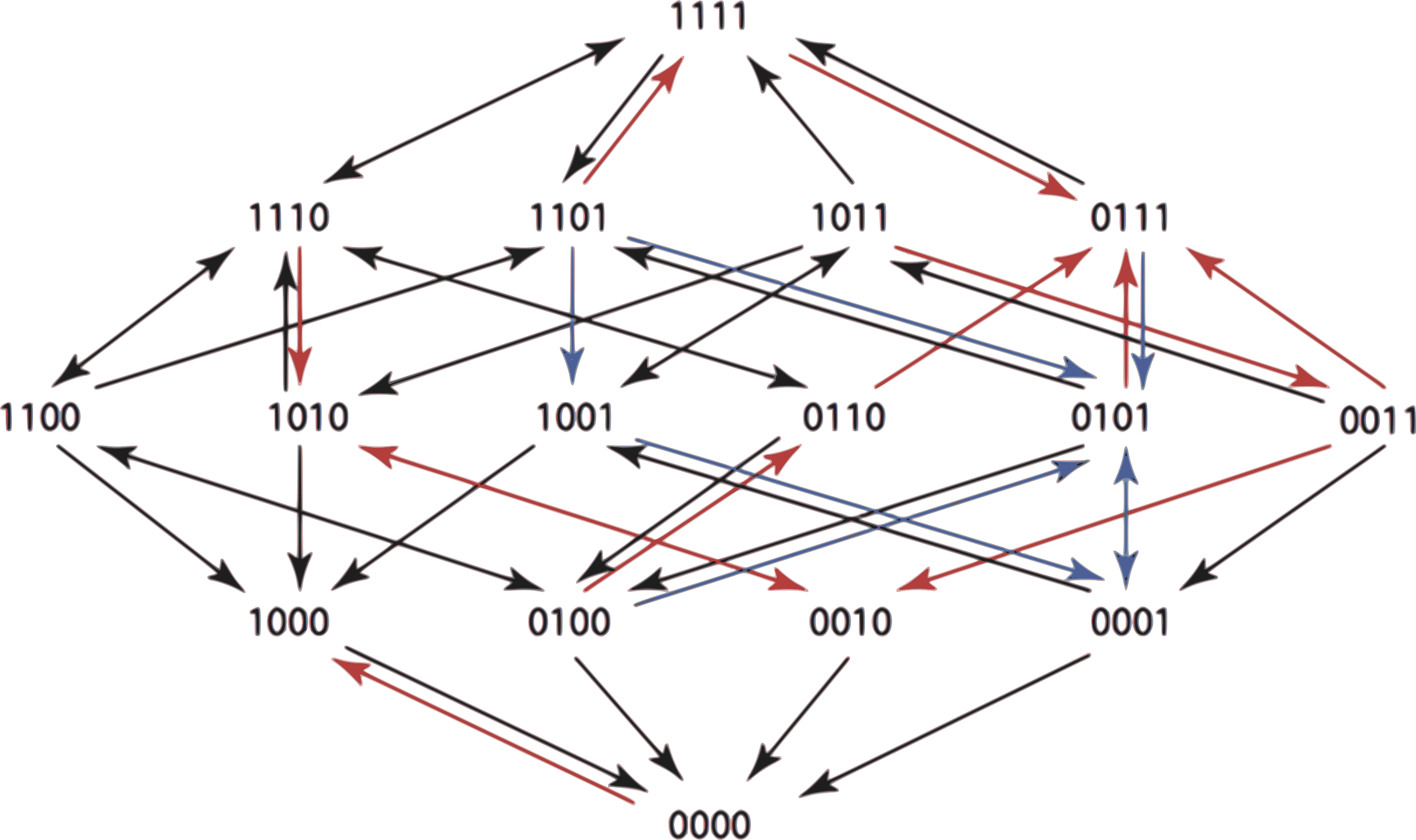
Вы также можете упорядочить эти данные в тензор 2 x 2 x 2 x 2. то есть 4-мерный массив, дающий ландшафт пригодности для генотипов под данным антибиотиком. В исследовании использовалось 15 антибиотиков, поэтому имеется 15 фитнес-тензоров. Если вы вводите последовательность антибиотиков, то общий ландшафт пригодности определяется составом их тензоров. Проблема состоит в том, чтобы найти оптимальную последовательность из k антибиотиков, такую, чтобы составной тензор пригодности C максимизировал вероятность перехода от любого генотипа u к дикому типу 0000.
Составной график Хэмминга для 6-шагового плана, показывающий пути от 1111 до 0000. Вы можете видеть, что в новом пейзаже фитнеса стрелки указывают обратно на дикий тип.
Это требует поиска всех 15k последовательностей длины k. Это большая проблема, но ее можно решить для k до 6, используя полное перечисление в программе Maple. Ключевое наблюдение, если вы хотите принять участие:
Программа работает медленно из-за экспоненциального роста числа последовательностей. В настоящее время мы не знаем, существует ли эффективный алгоритм для решения нашей задачи оптимизации для больших значений k.
Были опробованы два типа оптимизации. В первом использовались только направления стрелок, а во втором — фактические темпы роста. Использование фактических темпов роста дало лучшие результаты, и можно было найти шесть планов шагов, которые возвращали любой генотип в дикое состояние с вероятностью не менее 0,6.
Дело здесь в том, что эти планы вернут устойчивую популяцию обратно в дикое состояние, а затем сохранят дикое состояние нетронутым, позволяя врачу использовать антибиотики для убийства членов популяции.
В будущем исследователи планируют опробовать планы лечения в клинических условиях, а также поработать над улучшенными инструментами оптимизации.
Есть и другие очевидные возможности использования направленной эволюции таким образом. Возможно, нам удастся избежать размножения устойчивых сорняков и насекомых путем чередования обработок. Также могут быть способы вернуть экосистемы в естественное состояние, применив оптимальную циклическую обработку — своего рода суперпродукт севооборота.
«Дисковый метод определения чувствительности», Нетха Хусейн.
Это вполне может быть генетический алгоритм, который имеет значение.